المستوى الاعدادي

درس الجذور المربعة – السنة الثالثة إعدادي

يونيو 8, 2025
كوم 0

الأهداف التعليمية:

تعريف الجذر التربيعي وتمثيل هندسي له
تعلم خصائص الجذور التربيعية
إتقان حساب الجذور التربيعية للأعداد المربعة الكاملة
تطبيق قواعد العمليات على الجذور التربيعية

في هذا الدرس سنتعرف على مفهوم الجذر التربيعي وخصائصه الأساسية، مع تمارين تطبيقية وفق المنهاج المغربي.

1. تعريف الجذر التربيعي

الجذر التربيعي لعدد موجب a هو العدد الموجب الذي إذا ضرب في نفسه يعطي العدد a.

$\sqrt{a} = x \quad \text{حيث} \quad x^2 = a$

أمثلة:

العدد	الجذر التربيعي
$25$	$5$ لأن $5^2=25$
$16$	$4$ لأن $4^2=16$
$9$	$3$ لأن $3^2=9$

ملاحظة:

الجذر التربيعي لعدد موجب يكون دائما موجبا
لا يوجد جذر تربيعي للأعداد السالبة في مجموعة الأعداد الحقيقية

2. خصائص الجذور التربيعية

ليكن a و b عددين حقيقين موجبين لدينا :

$\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}$
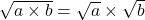
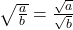$\sqrt{\frac{a}{b}} = \frac{\sqrt{a}}{\sqrt{b}}$ (b ≠ 0)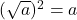
$(\sqrt{a})^2 = a$
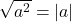$\sqrt{a^2} = |a|$ (قيمة مطلقة)

3. العمليات على الجذور المربعة

أ. الجمع والطرح

يمكن جمع أو طرح الجذور المتشابهة فقط مثال:

$3\sqrt{5} + 2\sqrt{5} = 5\sqrt{5}$
$\sqrt{a} + 3\sqrt{a} = 4\sqrt{a}$
$7\sqrt{3} - 4\sqrt{3} = 3\sqrt{3}$

ب. الضرب

$\sqrt{3} \times \sqrt{12} = \sqrt{36} = 6$
$2\sqrt{5} \times 3\sqrt{2} = 6\sqrt{10}$

ج. القسمة

$\frac{6\sqrt{15}}{2\sqrt{5}}} = 3\sqrt{3}$
$\frac{\sqrt{18}}{\sqrt{2}} = \sqrt{9} = 3$

4. تمارين تطبيقية

التمرين 1

احسب: $\sqrt{49}$
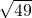
أوجد: $\sqrt{\frac{1}{16}}$

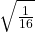
التمرين 2

بسّط: $\sqrt{50}$
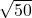
احسب: $2\sqrt{8} + 3\sqrt{2}$

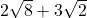
التمرين 3

حل المعادلة: $x^2 = 64$
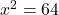
أوجد قيمة: $\sqrt{3^2 + 4^2}$

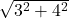
حلول التمارين

التمرين	الحل
$\sqrt{49}$	$7$
$\sqrt{\frac{1}{16}}$	$\frac{1}{4}$
$\sqrt{50}$	$5\sqrt{2}$
$2\sqrt{8} + 3\sqrt{2}$	$7\sqrt{2}$
$x^2 = 64$	$x = 8$ أو $x = -8$
$\sqrt{3^2 + 4^2}$	$5$

اختبر نفسك حول الجذور التربيعية ..

اترك بصمتك إلغاء الرد